AVL (Adel’son-Vel’skii Landis) – Árboles binarios Balanceados
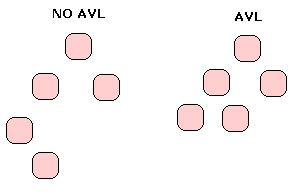
Posted: diciembre 7th, 2008 | Author: admin | Filed under: Algoritmos, C/C++, Estructuras de datos, Software, TAD | Tags: arbol binarios, arboles balanceados, avl, balanceo de avl, balanceo ll, balanceo rr, factor de balanceo, orden de acceso | Comentarios desactivados en AVL (Adel’son-Vel’skii Landis) – Árboles binarios BalanceadosLos árboles binarios tienen la utilidad de ordenar la información, separando el conjunto en dos posibilidades, izquierda y derecha, por lo que reducimos el conjunto de búsqueda a la mitad en cada paso. Esto nos lleva a que en un árbol balanceado (si tiene las ramas izquierda y derecha del mismo tamaño +1 o -1) tenemos una altura de Log(n), lo cual hace que las búsquedas sean «rápidas». El problema que tienen los árboles comunes es que pueden degenerar rapidamente en una lista, por ejemplo si insertamos el elemento 1 como raíz, y luego insertamos los números 2, 3, 4, 5… Tendremos inserciones siempre a la derecha, lo que nos lleva a tener una estructura de lista perdiendo la utilidad de dividir a la mitad en cada paso. Para solucionar esto utilizaremos los AVL, o árboles binarios balanceados, que nos permiten después de cada inserción rotar los nodos de forma de que quede ordenado.
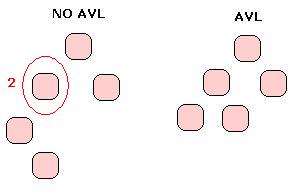
Los AVL utilizan el factor de balanceo para decidir si es necesario rotar una rama luego de insertar. Este FB (factor de balanceo) nos dice la diferencia de alturas entre el subárbol izquierdo y el derecho, por lo que restando las alturas de los mismos obtenemos este valor.
FB = Altura Subarbol Izquierdo – Altura Subarbol Derecho
En el primer ejemplo del caso anterior tenemos que la primer rama izquierda tiene un desbalanceo, ya que la altura de su subrama izquierda es 2, y la de la derecha es 0, lo que nos da: FB = 2. Tenemos desbalance. En el segundo caso el FB no supera el valor 1, por lo que no hay necesidad de rotar.
Las rotaciones se dividen en dos casos, simples o dobles. Las simples se conocen como LL si son de la rama izquierda, y RR si son de la rama derecha. Las rotaciones dobles son LR o RL, ya que son combinadas y más complejas como sugiere su nombre. Vemos primero las rotaciones simples.
En el caso simple LL, tomemos un nodo 1 que quedará con FB = 2, insertamos un nodo en el subárbol izquierdo de su hijo izquierdo, con lo que tenemos una inserción en la izquierda-izquierda (por eso Left Left). Para balancear el árbol deberemos tomar el hijo izquierdo de 1 (llamémoslo 2), y ponerlo como padre de 1, el hijo derecho de 1 queda en su lugar, el hijo izquierdo de 2 queda en su lugar y el hijo de derecho de 2 debe ir como hijo izquierdo de 1, ya que en su lugar tendremos a 1. Veamos un dibujo:
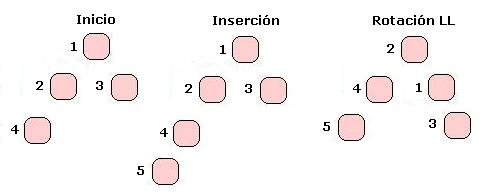
Lo que hacemos es mover el subárbol que queda con un largo excesivo hacia arriba, sacando al padre para hacer lugar, teniendo cuidado eso si de mantener la relación de mayor menor, lo cual hacemos dejando los subárboles izquierdos de 2 y derecho de 1 en sus lugares (ya que son menores que todos los demas, y mayores respectivamente), y moviendo de lugar el subárbol derecho de 2 hacia el izquierdo de 1. Esto lo podemos hacer ya que este subárbol contiene elementos mayores que los de 2, pero menores que 1.
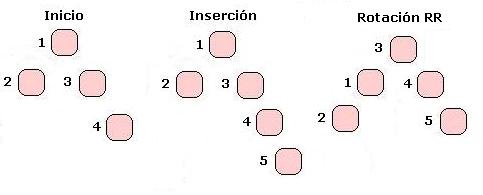
En el caso de la rotación simple RR sucede lo mismo que acabamos de ver, solo que en el caso de insertar a la derecha del hijo derecho:
Hemos visto los dos casos simples, donde insertamos en la rama menor que todos o mayor que todos. Veremos ahora que sucede cuando insertamos en el hijo derecho del subárbol izquierdo, o en el izquierdo del derecho, es decir cruzado.
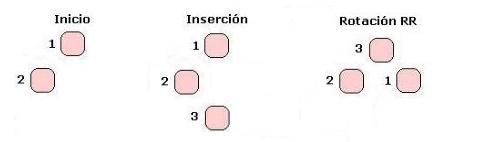
En este caso lo que haremos será aplicar dos rotaciones simples, con lo cual haremos que el nodo insertado «suba» acortando la altura del árbol. Noten que el nodo que tiene FB = 2 es el nodo 1, y no el nodo 2 que es donde insertamos (en su subárbol derecho). Por lo cual deberemos modificar la altura de sus hijos para reducir el FB a 1.
El proceso que seguiremos será el siguiente, tomamos el nodo en la rama donde se generó el desbalance, en este caso el 2, como la inserción es en el fijo derecho de 2, tomamos este nodo (el 3), y lo guardamos como la nueva raiz. Guardamos los dos hijos del 3 (ya que en realidad el árbol puede ser más amplio, y haber nodos hacia «abajo») y ponemos como su hijo izquierdo a 2, y su hijo derecho a 1. Así sabemos que el orden se mantiene, 3, estaba a la derecha de 2, por lo que es mayor, y a la izquierda de 1, por lo que es menor. Colocado 3 en el lugar de 1, tomamos los dos posibles hijos de 3 que guardamos y los colocamos respectivamente como hijo derecho de 2 al hijo izquierdo, y como hijo izquierdo de 1 al derecho de 3. Otra vez manteniendo el orden.
Veamos un ejemplo gráfico:
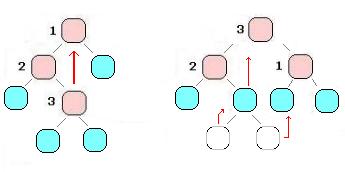
En resumen la idea es, cuando detectamos que un nodo tiene FB = 2 (recuerden, en valor absoluto), entonces de acuerdo a sea positivo o negativo tomamos la rama izquierda o la derecha, subimos el nodo correspondiente y reasignamos con cuidado los hijos para no perder el orden. Las operaciones LR y RL, como las LL y RR son simétricas, por lo que el código será idéntico cambiando el hijo seleccionado. Como mencionabamos antes, las operaciones complejas se pueden reducir a dos operaciones simples, por ejemplo la LR podemos reducrila a realziar primero una RR en el hijo izquierdo y luego una LL en la raíz.
Pasemos a los ejemplos de código en C para ver como implementar estas rotaciones.
Lo primero que tenemos que hacer, es hacer una modificación al tipo de dato de árbol binario, ya que queremos tener en cuenta el FB en cada nodo, para detectar un desbalance. Agregaremos un campo int con la altura del nodo actual, lo cual nos permite saber sin tener que sumar recursivamente cada vez la altura de un nodo con sus hijos:
struct AVLNode {
int dato;
AVLNode izq;
AVLNode der;
int altura;
};
El siguiente paso es agregar una función que nos permite conocer la altura de un nodo actual, de forma que nuestro TAD quede bien estructurado, y en caso de ser necesario poder actualizar la misma calculando el FB:
int Altura (AVLNode* t) {
if(t == NULL)
return -1;
else
return t->altura;
}AlturaCalcular (AVLNode* t) {
if(t != NULL)
t->altura = max (altura ((t)->izq), altura ((t)->der)) + 1;
}
Veamos el caso de una rotación simple RR:
void RotarAVLDer (AVLNode* &t) {
nodoAVL *taux;taux = t->right;
t->right = taux->left;
taux->left = t;actualizarAlturaAVL(t);
actualizarAlturaAVL(taux);t = taux;
}
Como ven, pasamos la raíz por referencia, de forma que podemos modificar el puntero y colocar su hijo derecho en su lugar. Pero primero tenemos cuidado de copiar los datos necesarios para no perder las referencias, y de actualizar las alturas correspondientes. Ahora veamos el caso de la rotación doble, para la cual usaremos el hecho de que podemos descomponer la misma en dos rotraciones simples.
void RotarAVLDerDoble (AVLNode* t) {
RotarAVLIzq(&(t)->der);
RotarAVLDer(t);
}
Primero realizamos una LL y luego una RR, RotarAVLIzq es la rotación simple en el hijo izquierdo, análoga a RotarAVLDer que acabamos de ver pero sobre el hijo izquierdo de la raíz.
Con esto tenemos las operaciones básicas para balancear, crearemos una funcion que nos permita balancear cuando lo necesitemos, y luego veremos la de inserción que será simple ya que tenemos las tareas divididas en nuestro TAD AVL.
void BalancearAVL (AVLNode* t) {
if(t != NULL) {
if (Altura(t->izq) – Altura(t–>der) == 2) { /* FB indica izquierda */
if (altura (t->izq->izq) >= altura (t->izq->der))
/* simple hacia la izquierda */
RotarAVLIzq(t);
else
/* doble hacia la izquierda */
RotarAVLIzqDoble(t);
}else if (Altura(t->der) – Altura(t->izq) == 2) { /* FB indica derecha */
if (Altura(t->der->der) >= Altura(t->der->izq))
/* simple derecha */
RotarAVLDer (t);
else
/* doble derecha */
RotarAVLDerDoble (t);
}
}
}
Y por último la inserción:
void InsertarAVL (AVLNode* t, int x) {
if (t == NULL) {
t = ArbolCrearAVL();
ArbolInsertar(t,x);
} else {
if (x < ArbolRaiz(t))
InsertarAVL(&t->izq, x);
else
InsertarAVL(&t->der, x);BalancearAVL(t);
AlturaCalcular (t);
}
}
Al insertar buscamos la posición del elemento como lo hacemos normalmente en un árbol binario, buscando en derecho o izquierda de acuerdo a la comparación. Una vez que encontramos su posición creamos un nuevo nodo y lo insertamos, al regresar de la recursión debemos balancear los nodos ya que podríamos haber creado un desbalance, actualizando la altura según corresponda.
Con esto completamos nuestro TAD AVL, como ya dijimos tenemos la capacidad de ordenar el árbol y asegurarnos que el orden de búsqueda de un elemento no supere nunca Log(n). Un buen ejercicio de multiestructuras es pensar en la combinación de un AVL con una lista, de forma que podamos buscar determinado valor dentro del AVL, y luego a partir de ese valor podamos recorrer una cantidad de valores ordenados sin tener que buscar cada uno.
Supongamos que tenemos tiempos ordenados en un AVL, y queremos obtener los 10 tiempos siguiente a partir de cierto momento. Entonces lo que podemos hacer es tener un AVL «espejado» en una lista, con lo cual podemos buscar el tiempo deseado en el AVL (o el más cercano a él), y luego de encontrar el mismo saltamos a la lista (mantendremos un puntero a la posición correspondiente en cada nodo del AVL) y recorremos la lista obteniendo los 10 elementos. Así logramos un buen grado de eficiencia, teniendo únicamente que buscar un tiempo en el AVL con un orden Log(n) y luego recorriendo la lista que ya sabemos esta ordenada ya que mantenemos el orden al hacer cada inserción.
En la próxima entrada veremos las tablas de dispersión o Hash, los cuales nos permite hacer búsquedas en un tiempo constante.